Laboratories

AI in Optoacoustics

The biomedical imaging workflow

Research Outline

Figure 2. Optoacoustic signal variation over light fluence with different absorption coefficient. Taken from J. Malekzadeh, et. al. J. Biophoton. (in press).

High-quality biomedical imaging needs mathematical reconstruction procedures that are accurate and efficient at the same time, and subsequent data analysis that is reliable and insightful.

At the group for mathematical modelling and inverse problems of CBI, we design innovative algorithms for biomedical imaging modalities based on sophisticated mathematical models. Our main focus is multispectral optoacoustic tomography (MSOT) and its combination with ultrasound imaging (OPUS). We also contribute to the analysis of the huge amount of data that is generated within the institute and in our research collaborations. Our goal is to drive the development towards quantitative optoacoustic and ultrasound imaging, thereby increasing the method's impact in translational medicine.

In close collaboration with the other groups at CBI - in particular with the group for machine learning in biomedical imaging and the group for multispectral optoacoustic tomography - we focus our research to the following three areas.

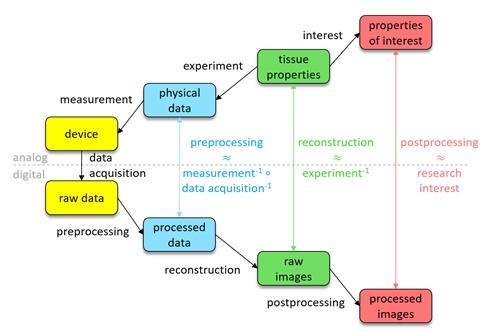
Mathematical modelling. In order to even formulate the problem of information extraction from imaging data, a proper model of the whole imaging process is necessary. To quantitatively and efficiently capture the different aspects of imaging, including the propagation of uncertainties, is the scope of mathematical modelling. In particular, in biomedical imaging, models for the probe, the optical and acoustic interaction of tissue and probe, the measurement, and the data acquisition are needed. Mathematics is not only the appropriate language for exact models, but provides diverse tools and concepts that allow to capture the validity of a model.

Figure 3. (a-b) MIP results of the L2-LSQR, L1-GDBT and L1-GDBB reconstructions form side and top view. (c) Zoomed-in images of the top view MIP results of the three reconstructions within dash-dot square box in (b). Taken from Y. Han et. al., Opt. Lett. 42(5), 979-982 (2017)

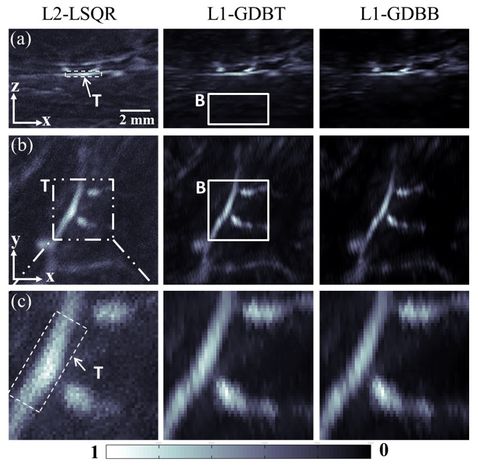
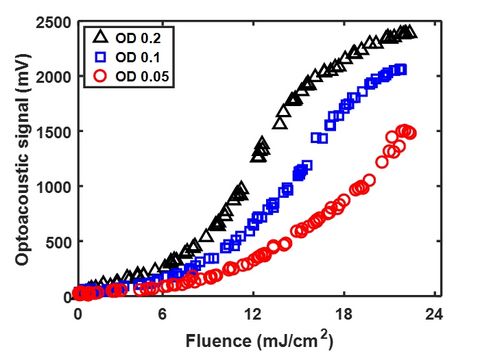
Inverse problems. The reconstruction of properties of interest from imaging data is an inverse problem, as it performs the inversion of a forward model of the imaging process. Abstractly, this problem can be divided into three steps: (1) preprocessing, which tries to approximate the physical response of the system by inverting data acquisition and measurement, (2) reconstruction, which tries to infer the tissue properties from the knowledge of the response by inverting the interaction, and (3) postprocessing, which extracts the properties of interest from the reconstruction. As most clinical applications ask for quantitative information, our goal is to not only retrieve the best possible estimate of the desired properties, but also to develop tools that reliably quantify the uncertainty of the reconstructions.

Figure 4. First 60 minutes VTP effect monitoring by MSOT. The tumors could be depicted clearly by MSOT (800 nm single wavelength images shown here; blue outline) and did not markedly change over the course of the first hour after WST11-VTP or sham treatment. However, a prominent vessel that is seen to cross the tumor before treatment onset, appeared morphologically destructed in its intratumoral course over the course of 60 minutes (arrows left panel) while the crossing tumor vessel in the control mouse appeared morphologically unchanged (arrows right panel). On SO2 mapping, reduced oxygen saturation in the perivascular tumor ROI (dotted circles) was monitored by MSOT relative to baseline, while in comparison no reduction was observed after saline-VTP sham treatment as control. Taken from V. Neuschmelting, et. al., Theranostics (in press).

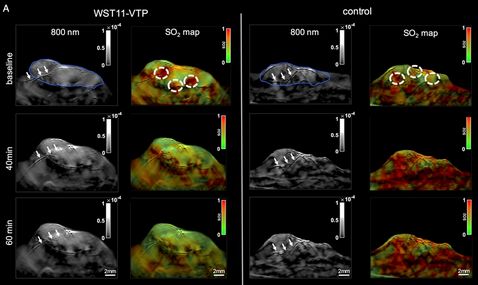
Data analysis. In order to extract clinically relevant information from the reconstructed data, it needs to be organized, structured, and analysed. Advances in computational science and data science, in particular in statistical learning, provide a rich toolbox for these purposes. We aim at further improving these methods and optimally adapting them to our needs. In addition, data can be used to improve the modelling and inversion steps by data-driven methods. For example, an efficient low-dimensional model for the class of structures of interest could be derived from the data.